Affinity Propagation#
모든 데이터가 특정한 기준에 따라 자신을 대표할 대표 데이터를 선택한다. 만약 스스로가 자기 자신을 대표하게 되면 클러스터의 중심이 된다.
responsibility \(r(i, k)\)
\(k\)번째 데이터가 \(i\)번째 데이터의 대표가 되어야 한다는 근거
availability \(a(i, k)\)
\(i\)번째 데이터가 \(k\)번째 데이터를 대표로 선택해야 한다는 근거
responsibility와 availability를 모두 0으로 놓고 다음 수식을 수렴할 때까지 반복
\[ r(i, k) \leftarrow s(i, k) - \max_{k' \neq k} ( a(i, k') + s(i, k')) \]
\[ a(i, k) \leftarrow \min(0, r(k, k) + \sum_{i' \neq i,k} r(i', k)) \]
여기에서 \(s(i,k)\)는 다음과 같이 음의 거리로 정의되는 유사도이다.
\[ s(i,k) = -|| x_i - x_k ||^2 \]
특히 \(s(k,k)\)는 특정한 음수 값으로 사용자가 정해 주게 되는데 이 값에 따라서 클러스터의 갯수가 달라지는 하이퍼 모수가 된다. \(s(k,k)\)가 크면 자기 자신에 대한 유사도가 커져서 클러스터의 수가 증가한다.
위 알고리즘으로 계산하는 \(r\), \(a\)가 더 이상 변화하지 않고 수렴하면 계산이 종료되고 종료 시점에서 \(r(k,k) + a(k,k) > 0\)이 데이터가 클러스터의 중심이 된다.
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import AffinityPropagation
from sklearn.metrics import *
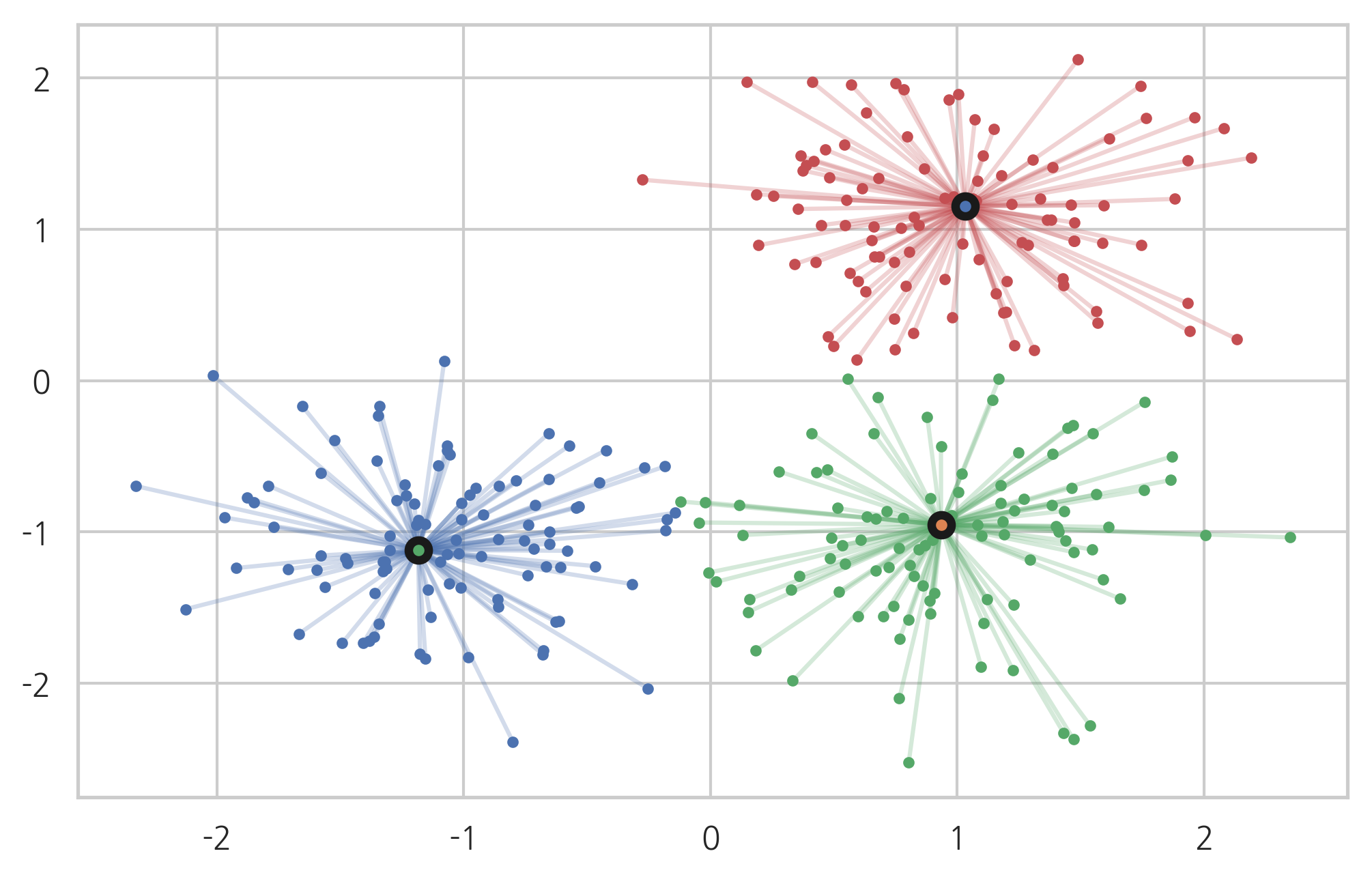
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=300, centers=centers, cluster_std=0.5, random_state=0)
model = AffinityPropagation(preference=-50).fit(X)
cluster_centers_indices = model.cluster_centers_indices_
labels = model.labels_
n_clusters_ = len(cluster_centers_indices)
print('Estimated number of clusters: %d' % n_clusters_)
print("Adjusted Rand Index: %0.3f" % adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f" % adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f" % silhouette_score(X, labels, metric='sqeuclidean'))
Estimated number of clusters: 3
Adjusted Rand Index: 0.912
Adjusted Mutual Information: 0.871
Silhouette Coefficient: 0.753
from itertools import cycle
colors = cycle('rgb')
for k, col in zip(range(n_clusters_), colors):
class_members = labels == k
cluster_center = X[cluster_centers_indices[k]]
plt.plot(X[class_members, 0], X[class_members, 1], col + '.')
for x in X[class_members]:
plt.plot([cluster_center[0], x[0]], [cluster_center[1], x[1]], col, alpha=0.25)
plt.plot(cluster_center[0], cluster_center[1], 'o', mec='k', mew=3, markersize=7)
plt.show()